2025年05月15日 06:54

什么是微元法？微元法的定义、原理与应用详解

一、微元法的定义

微元法（Differential Element Method）是一种通过分析无限小量（微元）来研究连续变化现象的数学工具，广泛应用于物理学、工程学和高等数学领域。其核心思想是将复杂问题拆解为无数个简单、可描述的微小单元，通过数学积分或微分手段，从局部规律推导整体性质。

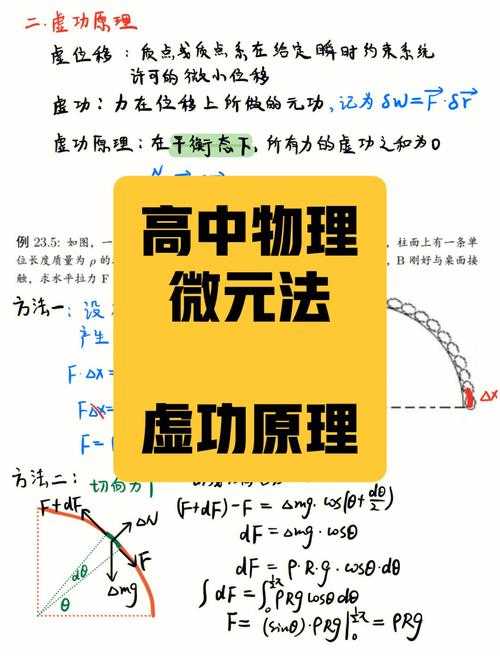
（什么是微元法？微元法的定义、原理与应用详解）

例如，计算一根非均匀密度细杆的质量时，传统方法难以直接求解，但若将细杆分割为无数长度趋近于零的微元段，每段质量可表示为 \\( dm = \\rho(x)dx \\），再积分求和，就能精确得出总质量。这种“化整为微，积微成宏”的思路，正是微元法的精髓。

二、微元法的原理

微元法的理论基础源自微积分学中的极限思想，遵循以下步骤：

1. 选取微元：在研究对象中选取一个特征明显的微小单元，例如一段弧长 \\( ds \\)、体积元 \\( dV \\)，或时间微元 \\( dt \\)。

2. 描述局部规律：根据物理定律或几何关系，建立微元满足的数学关系式（如 \\( dF = \\rho g \\cdot dV \\））。

3. 积分求解整体量：通过积分操作将微元表达式扩展到整个研究范围（如 \\( F = \\int \\rho g \\, dV \\））。

关键原则：

物理真实性：微元需足够小，使其内部性质均匀；

数学严谨性：高阶无穷小量可忽略，简化计算；

边界适配性：积分上下限需与实际物理范围严格对应。

三、微元法的典型应用场景

1. 物理学中的经典问题

变力做功：当力随位移变化时（如弹簧压缩），功的计算公式 \\( W = \\int F(x) dx \\）直接源于微元法。

转动惯量计算：将刚体分解为质点微元，积分表达式 \\( I = \\int r2 dm \\）可求解复杂形状物体的转动惯量。

电场与磁场分析：通过电荷微元 \\( dq \\）或电流微元 \\( Idl \\），推导出库仑定律、毕奥-萨伐尔定律的积分形式。

2. 工程学中的实际问题

流体力学：计算管道中流体的流量时，选取横截面速度微元 \\( v(r) \\），总流量 \\( Q = \\int_0R 2\\pi r v(r) dr \\）。

结构力学：分析梁的弯曲应力分布时，通过微元受力平衡方程建立微分关系。

热传导分析：利用温度梯度微元 \\( dT/dx \\），推导傅里叶热传导定律的微分形式。

3. 高等数学的拓展应用

曲线弧长计算：将曲线近似为无数直线微元，弧长公式 \\( S = \\int \\sqrt{1+(dy/dx)2} dx \\）。

旋转体体积：通过圆盘法或壳层法建立体积微元 \\( dV \\），积分求解复杂旋转体体积。

微分方程建模：将动态过程离散为时间微元，建立速率方程（如人口增长模型 \\( dP/dt = kP \\））。

四、微元法的优势与局限

优势：

直观性强：物理意义明确，避免抽象符号运算；

适应复杂边界：可处理非对称、非均匀的实际问题；

统一方法论：贯穿力学、电磁学、热学等多学科。

局限：

依赖坐标系选取：不同坐标系下微元表达式差异较大（如柱坐标中体积元 \\( dV = r dr d\ heta dz \\））；

高阶效应忽略风险：若微元内部变化剧烈（如冲击波前沿），可能导致结果偏差；

积分难度制约：某些情况下积分无解析解，需依赖数值方法。

五、权威教材与科研领域的认可

微元法是清华大学《大学物理》、同济大学《高等数学》等国家级规划教材的核心内容，也是MIT公开课《经典力学》推荐的基础工具。在科研领域，NASA喷气推进实验室（JPL）的轨道力学仿真、ANSYS有限元分析软件的前处理模块，均以微元法为底层逻辑。普林斯顿大学物理学教授Richard Feynman曾评价：“微元法是人类理解连续介质行为最锋利的思维刀具。”

总结：微元法通过“分解-建模-重构”的三步策略，将复杂连续问题转化为可操作的数学表达式。掌握该方法，需深入理解微积分思想，并结合具体物理场景反复训练。这一工具不仅在学术研究中不可或缺，更是工程师解决实际问题的“标准动作”。